On Dirichlet hyperbola method

Date [ Mon, 04 Aug 2025 23:00:09 +0800 ]

Dirichlet Convolution

We are going to deal with this kind of sum:

$$\sum_{d|n} f(d) g(\frac{n}{d})$$

Some examples are:

$$\varphi(n) = \sum_{d|n} \mu(d) \frac{n}{d}$$

and

$$n = \sum_{d|n} \varphi(d)$$

The sums above are actually known as the Dirichlet convolution, which can be formally written as

$$(f * g)(n) = \sum_{d|n} f(d) g(\frac{n}{d})$$

If we let $\textbf{1}(n) = 1$ and $\textbf{Id}(n) = n$, then our examples can be rewritten as $\varphi = \mu * \text{Id}$ and $\text{Id} = \varphi * \text{1}$.

We can then also observe from the examples that $\mu$ and $\text{1}$ are inverses of each other. A Dirichlet inverse $f^{-1}$ is a function such that $f * f^{-1} = \varepsilon$, where $\varepsilon(n) = 1$ when $n = 1$, otherwise $\varepsilon(n) = 0$. To put more concisely, $\text{1} * \mu = \varepsilon$.

Hyperbola Method

Suppose we want to compute $$\sum_{i=1}^n (f * g)(i) = \sum_{ij \leq n} f(i) g(j)$$

Visually, we want to sum the lattice point values under the curve $y = \frac{n}{x}$, where the point $(x, y)$ has a value of $f(x) g(y)$. Below, we are going to sum the blue area, the red area, then subtract the double-counted square at the corner.

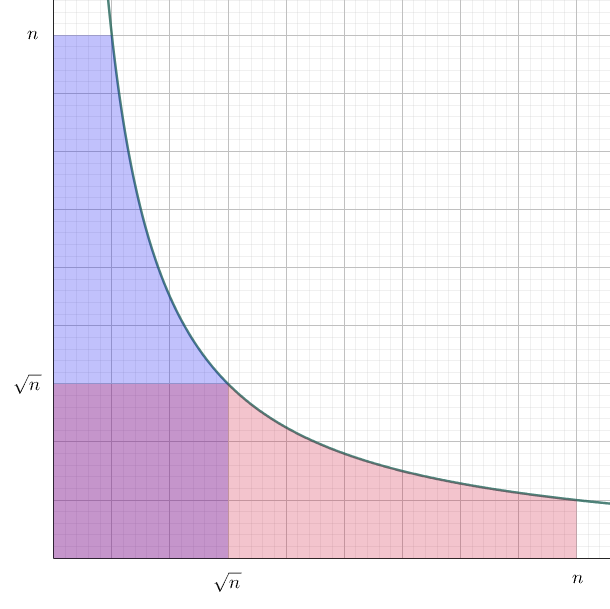
Let $F$ and $G$ be the prefix sum of $f$ and $g$ respectively. Formally, $F(n) = f(1) + … + f(n)$. Then,

$$\sum_{ij \leq n} f(i) g(j) = \sum_{i=1}^{\lfloor \sqrt n \rfloor} f(i) G\left(\left\lfloor\frac{n}{i}\right\rfloor\right) + \sum_{j = 1}^{\lfloor \sqrt n \rfloor} F\left(\left\lfloor\frac{n}{j}\right\rfloor\right) g(j) - F(\lfloor \sqrt{n} \rfloor) G(\lfloor \sqrt{n} \rfloor)$$

which can be computed in $\mathcal{O}(\sqrt{n})$ operations (assuming all of $f$, $g$, $F$, and $G$ are easy to compute).

In a lot of cases, it’s either $F(n)$ or $G(n)$ that is hard to compute, so let’s rearrange the equation above so that $F(n)$ is at the left-hand side of the equation.

$$F(n) g(1) = \sum_{ij \leq n} f(i) g(j) + F(\lfloor \sqrt{n} \rfloor) G(\lfloor \sqrt{n} \rfloor) - \sum_{i=1}^{\lfloor \sqrt n \rfloor} f(i) G\left(\left\lfloor\frac{n}{i}\right\rfloor\right) - \sum_{j=2}^{\lfloor \sqrt n \rfloor} F\left(\left\lfloor\frac{n}{j}\right\rfloor\right) g(j)$$

There are $\mathcal{O}(\sqrt{n})$ different values of $\left\lfloor\frac{n}{i}\right\rfloor$, so $F$ can be computed in the increasing order of $\left\lfloor\frac{n}{i}\right\rfloor$. In fact, if we have precomputed $F(i)$ for $i < n^{2/3}$, then $F(n)$ can be computed in $\mathcal{O}(n^{2/3})$ operations.

Euler Summatory Function

Let’s take an example by trying to compute

$$\Phi(n) = \sum_{i=1}^n \varphi(i)$$

We are going to make use of $\text{Id} = \varphi * 1$. We note that $\sum_{i=1}^n \text{Id}(i) = \frac{n(n+1)}{2}$ and $\sum_{i=1}^n \text{1}(i) = n$, so they are easy to compute.

Applying the hyperbola method, we obtain:

$$\Phi(n) = \frac{n(n+1)}{2} + \lfloor\sqrt{n}\rfloor \Phi(\lfloor\sqrt{n}\rfloor) - \sum_{i=1}^{\lfloor\sqrt{n}\rfloor} \varphi(i) \left\lfloor\frac{n}{i}\right\rfloor - \sum_{j=2}^{\lfloor\sqrt{n}\rfloor} \Phi\left(\left\lfloor\frac{n}{j}\right\rfloor\right)$$

So $\Phi(n)$ can be computed in sublinear time.

A sample implementation in Python can be seen as follows.

@functools.cache
def Phi(n):
    if n < PRECOMPUTED:
        return _Phi[n]

    sn = math.isqrt(n)
    ret = n*(n+1) // 2 + sn*Phi(sn)
    ret -= sum(_phi[i] * (n//i) for i in range(1, sn+1))
    ret -= sum(Phi(n//i) for i in range(2, sn+1))
    return ret

You can attempt with your own implementation on this Library Checker.

Mertens Function

We will try to compute:

$$M(n) = \sum_{i=1}^n \mu(i)$$

By noting that $1 * \mu = \varepsilon$, we can then apply the hyperbola method and obtain:

$$M(n) = 1 + \lfloor \sqrt{n} \rfloor M(\lfloor \sqrt{n} \rfloor) - \sum_{i=1}^{\sqrt{n}} \mu(i) \left\lfloor \frac{n}{i} \right\rfloor - \sum_{j=2}^{\sqrt{n}} M\left(\left\lfloor\frac{n}{j}\right\rfloor\right)$$

so $M(n)$ can be computed in sublinear time.

Other interesting properties that you may find infer from $1 * \mu = \varepsilon$ are:

$$1 = \sum_{k=1}^n \mu(k) \left\lfloor\frac{n}{k}\right\rfloor = \sum_{k=1}^n M\left(\left\lfloor\frac{n}{k}\right\rfloor\right)$$

Project Euler #319

You can read the problem here.

Without diving deep into the math details, the quantity we are looking for can be computed by the following.

def solve(n):
    a = [3**i - 2**i for i in range(n)]
    for i in range(1, n):
        for j in range(i*2, n, i):
            a[j] -= a[i]
    return sum(a)

Of course, it can get pretty slow when $n = 10^{10}$, so we have to do something about it.

Let $f(n) = 3^n - 2^n$. We can see that the function solve is doing a Möbius transform on $f$ then computes its sum. To put more concisely, we are trying to evaluate

$$\sum_{i=1}^n (f * \mu)(i)$$

There are two approaches here, and they both involve the hyperbola method.

First approach

First, we compute the Mertens function $M\left(\left\lfloor\frac{n}{i}\right\rfloor\right)$ for all possible values of $\left\lfloor\frac{n}{i}\right\rfloor$ (there are around $2\sqrt{n}$ of them) using the hyperbola method. Also note that $F(n) = f(1) + f(2) + … + f(n)$ has an $\mathcal{O}(1)$ formula. Then, apply the hyperbola method again to compute the final sum:

$$\sum_{i=1}^{\lfloor\sqrt{n}\rfloor} f(i) M\left(\left\lfloor\frac{n}{i}\right\rfloor\right) + \sum_{j=1}^{\lfloor\sqrt{n}\rfloor} F\left(\left\lfloor\frac{n}{j}\right\rfloor\right) \mu(j) - F(\lfloor\sqrt{n}\rfloor) M(\lfloor\sqrt{n}\rfloor)$$

This requires two hyperbola methods, which are already sufficient, but we can do something simpler.

Second approach

Let $g = f * \mu$, we can rewrite it as $f = g * \text{1}$. We want the value of $G(n) = g(1) + g(2) + … + g(n)$ which can be computed by the hyperbola method:

$$G(n) = F(n) + \lfloor\sqrt{n}\rfloor G(\lfloor\sqrt{n}\rfloor) - \sum_{i=1}^{\sqrt{n}} g(i) \left\lfloor\frac{n}{i}\right\rfloor - \sum_{j=2}^{\sqrt{n}} G\left(\left\lfloor\frac{n}{i}\right\rfloor\right)$$

which solves the problem.

Dirichlet Series

I will briefly mention the Dirichlet series here.

The Dirichlet series for a function $f$ can be defined as follows.

$$F(s) = \sum_{n \geq 1} \frac{f(n)}{n^s}$$

So if we have $h = f * g$, then $H(s) = F(s)G(s)$! Here are a few examples of the Dirichlet series.

$\zeta(s)$: the Riemann zeta function is a Dirichlet series for $\text{1}$.
$\frac{1}{\zeta(s)} = \sum_{n \geq 1} \frac{\mu(n)}{n^s}$ by noting that $1$ and $\mu$ are inverses of each other.
$\zeta(s-1)$ is a Dirichlet series for $\text{Id}$.
$\zeta(s-a)$ is a Dirichlet series for $f(n) = n^a$.
$\frac{\zeta(s-1)}{\zeta(s)} = \sum_{n \geq 1} \frac{\varphi(n)}{n^s}$ by noting that $\varphi = \mu * \text{Id}$.

Interestingly, the formal power operations, such as $\exp$ and $\log$, can also be applied to the Dirichlet series, and one can show that $\log \zeta(s)$ has a relation with the prime zeta function, which I will explore more in the next article (hopefully).